Menentukan Luas Permukaan Limas

Limas ialah berdiri ruang sisi datar yang alasnya berupa poligon (segi banyak) dan sisi tegaknya ialah segitiga yang berpotongan di satu titik, yaitu titik puncak Dalam kehidupan sehari-sehari, kita sering kali mendapat benda-benda yang berbentuk limas, misalnya: piramida, candi Prambanan atap rumah, atap menara dan lain-lain. Dua jenis limas yang sering kita temui ialah limas segiempat dan limas segitiga.

Limas persegi ialah limas yang dibatasi oleh sebuah persegi sebagai bantalan dan beberapa buah bidang berbentuk segitiga sebagai bidang tegak yang bertemu pada suatu titik puncak. Dengan ciri-ciri sebagai berikut:

• Alasnya berbentuk segiempat.
• Mempunyai lima buah bidang sisi.
• Memiliki lima buah titik sudut.
• Mempunyai delapan buah rusuk.

Jaring-jaring limas beraturan terdiri atas sebuah bantalan berbentuk persegi dan 4 buah sisi tegak yang berbentuk segitiga. Sehingga untuk menghitung luas permukaan limas persegi sanggup dilakukan dengan merebahkan sisi-sisi limas,  hasilnya ialah jaring-jaring limas (Lihat Gmb. Luas jaring-jaring inilah yang merupakan luas permukaan limas. Rumus luas permukaan limas persegi adalah:

Volume Limas = Alas x Tinggi
Luas Pemukaan Limas= Luas Alas + Jumlah luas sisi tegak.

Limas segitiga merupakan berdiri ruang yang berbentuk limas dengan bantalan yang berbentuk segitiga. Limas segitiga dibedakan menjadi dua jenis yakni limas segitiga beraturan dan limas segitiga sebarang. Ciri ciri limas segitiga.

• Mempunyai bantalan yang berbentuk segitiga.
• Memiliki empat buah bidang sisi yaitu bantalan dan tiga buah sisi tegak.
• Mempunyai enam buah rusuk.
• Memiliki empat buah titik sudut.

Rumus limas segitiga
Rumus luas bantalan limas = 1/2 x a x t
Rumus luas permukaan limas = luas bantalan +  jumlah luas seluruh sisi tegak
Rumus volume limas segitiga yaitu V = 1/3 x (1/2 x Alas x Tinggi) x Tinggi

Ayo Kita Amati
Diketahui bantalan limas tersebut berbentuk persegi dengan panjang TE = 5 cm dan AB = 6 cm. Apakah luas permukaannya sanggup ditentukan?

Soal tersebut sanggup diselesaikan, alasannya bentuk alasnya persegi dengan ukuran sisi 6 cm dan tinggi bidang tegaknya juga sudah diketahui ukurannya, yaitu 5 cm. Dengan demikian, selanjutnya tinggal cari luas permukaannya denga rumus:

L = luas bantalan + jumlah luas bidang tegak
L = 62 + 4 × 1/2 × 6 × 5
L = 36 + 60
L = 96 cm²

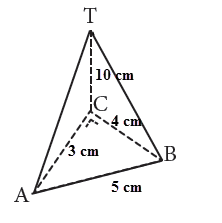
Sebuah limas alasnya berbentuk segitiga dengan panjang AC = 3 cm, BC = 4 cm, dan AB = 5 cm. Apabila tinggi limas 10 cm. Apakah luas permukaannya sanggup ditentukan?

Soal tersebut sanggup diselesaikan, alasannya bantalan limas tersebut berbentuk segitiga siku-siku dengan ukuran sudah diketahui. Sudah diketahui juga ukuran tinggi limasnya. Dengan demikian, selanjutnya luas masingmasing bidang, yaitu luas bidang ACB, bidang ACT, bidang BCT, dan bidang ABT. Khusus untuk mencari luas bidang ABT carilah terlebih dulu panjang AT dan BT dengan memakai Pythagoras

Ayo Kita Menalar
Berdasarkan aktivitas menggali info yang telah kalian dapatkan. Sekarang coba kalian jelaskan
bagaimana cara memilih ukuran bantalan suatu limas segiempat beraturan kalau diketahui luas permukaan limas tersebut ialah 360 cm² dan luas sisi tegaknya ialah 100 cm. Berapa banyak ukuran bantalan yang kalian temukan?

Luas Alas	Luas Sisi Tegak	Luas Permukaan
260 x 1 = 260	100 cm²	260 + 100 = 360 cm²
130 x 2 = 260	100 cm²	260 + 100 =360 cm²
65 x  4 = 260	100 cm²	260 + 100 = 360 cm²
52 x 5 = 260	100 cm²	260 + 100 = 360 cm²
26 x 10 = 260	100 cm²	260 + 100 = 360 cm²
13 x 20 = 260	100 cm²	260 + 100 = 360 cm²

Soal Latihan
1. Perhatikan limas segi empat beraturan K.PQRS di bawah. Sebutkan semua:

a. rusuk. rusuknya ada 8 yaitu : PQ; QR; RS; PS; KP;KQ; KR; dan KS
b. bidang sisi tegak. Segitiga KPQ; KQR; KSR; dan KPS
c. tinggi limas : KM

2. Kerangka model limas dengan bantalan berbentuk pergi panjang dengan panjang lebarnya masing-masing 16 cm dan 12 cm, sedangkan tinggi limas 24 cm. Tentukan panjang kawat yang diharapkan untuk menciptakan kerangka model limas tersebut.

3. Sebuah limas tingginya 36 cm dan tinggi rusuk tegaknya 39 cm. Jika alasnya berbentuk persegi maka tentukan:

a. keliling persegi = 120 cm
b. luas permukaan limas = 3.240 cm²

4. Alas sebuah limas berbentuk persegi dengan panjang sisi 12 cm. Jika jumlah luas sisi limas
384 cm², maka berapakah volume limas tersebut?

L. 4 segitiga = 384 - 12² = 384 - 144 = 240 cm²
L. segitiga = 240 : 4 = 60 cm²
t. segitiga = 2(60) : 12 = 10 cm
t. limas = √(10² - 6²) = √64 = 8 cm
V = 1/3 . 144 . 8 = 384 cm³

5. Gambar di bawah mengatakan sebuah kubus dengan panjang rusuk 5 cm yang dipotong
sehingga salah satu bagiannya beebentuk limas segitiga (tetrahedron). Tentukan luas permukaan kedua berdiri hasil perpotongannya.