Kesebangunan Dan Kongruensi Berdiri Segitiga

Kesebangunan yakni kesamaan perbandingan panjang sisi dan besar sudut antara dua buah berdiri datar atau lebih. Pengertian kesebangunan ibarat ini berlaku umum untuk setiap berdiri datar. Dua berdiri datar dikatakan sebangun bila panjang sisi-sisi yang bersesuaian dari kedua berdiri itu mempunyai perbandingan senilai dan sudut-sudut yang bersesuaian dari kedua berdiri itu sama besar.

Salah satu syarat kesebangunan yakni sudut-sudut yang bersesuaian sama besar. Artisama besar disini yakni ukuran sudutnya sebanding, Dua berdiri yang kongruen niscaya sebangun, tetapi dua berdiri yang sebangun belum tentu kongruen. Bangun-bangun yang mempunyai bentuk dan ukuran yang sama dikatakan bangun-bangun yang kongruen. Pengertian kekongruenan tersebut berlaku juga untuk setiap berdiri datar.

A. Dua Bangun Datar Sebangun
Dua buah berdiri dikatakan sebangun bila sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian mempunyai perbandingan yang sama. Beberapa berdiri yang niscaya sebangun diantaranya yakni dua segitiga samasisi, dua buah persegi, dua buah segi banyak beraturan, dan dua buah lingkaran.

Syarat Dua Segitiga Sebangun
Dua buah segitiga sanggup dikatakan sebangun bila memenuhi beberapa sayarat. Syarat segitiga dikatakan sebangun antara lain sebagai berikut.

1. Jika sudut-sudut yang bersesuaian dari dua buah segitiga sama besar.
2. Jika perbandingan sisi-sisi yang bersesuaian dari dua buah segitiga sama

Perbandingan Sisi-sisi Pada Segitiga Sebangun
Sisi-sisi yang bersesuaian pada dua segitiga yang sebangun yakni sebanding. Oleh alasannya yakni itu bila diketahui faktor skala perbandingannya maka kita sanggup mencari panjang sisi-sisi segitiga yang belum diketahui.

B. Segitiga Kongruen
Dua berdiri segitiga sanggup dikatakan kongruen apabila memenuhi beberapa sayarat. Sayara-syarat segtiga kongruen antara lain sebagai beriktu.

1. Jika panjang ketiga sisi dari dua segitiga sama panjang ( Sisi Sisi Sisi) atau (S S S)
2. Jika panjang dua sisi dan besar sudut yang diapit kedua sisi tersebut sama (Sisi Sudut Sisi) atau (S Sd S).
3. Jika besar dua buah sudut dan panjang sisi diantara kedua sudut dari dua segitiga sama (Sudut Sisi Sudut) atau (Sd S Sd).

C. Contoh Soal
Setelah membaca klarifikasi di atas untuk lebih memahami klarifikasi tersebut sanggup dilakukan dengan cara mengerjakan soal-soal latihan.

Contoh Soal 1
Selembar kertas berukuran ganjal 30  cm dan tinggi 40 cm dijadikan bingkai photo. Di sebelah kanan, kiri, dan atas photo masih ada sisa karton selebar 3 cm. Bila photo dan karton sebangun maka lebar karton bab bawah photo yang tidak tertutupi adalah....

Pembahasan :
Jika lebar karton bab bawah photo = x cm
Alas karton 30 cm
Alas Photo = 30 - (3 x 2) = 24 cm
Tinggi karton 40 cm
Karton dan photo sebangun sehingga :

Jawaban =	Alas Karton	=	Tinggi Karton
	Alas karton		Tinggi Karton

=	30	=	40	dengn perkalian silang T =	24 x 40	= 32
	24		T		30

Lebar bawah = 40 -3 - 32 = 5 cm.

Contoh Soal 2
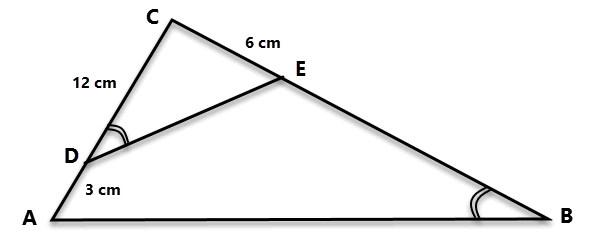
Perhatikan gambar di bawah ini.

Panjang BE adalah....

Pembahasan : ΔCDE dan ΔABC sebangun
∠ D = ∠B (diket)
∠C = ∠C (berimpit/seletak)
∠E = ∠A = (180° - ∠C - ∠D)

Jadi	CD	=	CE	=	DE
	BC		CA		BA

=	12	=	6	, BE + 6 =	12 x 15	= 30
	BE + 6		12 + 3		6

BE = 30 - 6 = 24 cm